Skip to contents

vanderPloeg2024_analysis

Source: vignettes/vanderPloeg2024_analysis.Rmd
vanderPloeg2024_analysis.Rmd

Introduction

In this vignette we examine and model the vanderPloeg2024 data in more detail.

library(parafac4microbiome)
library(dplyr)
#> 
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#> 
#>     filter, lag
#> The following objects are masked from 'package:base':
#> 
#>     intersect, setdiff, setequal, union
library(ggplot2)
library(ggpubr)

Processing the data cube

The data cube in vanderPloeg2024$data contains unprocessed counts. The function processDataCube() performs the processing of these counts with the following steps:

  • It performs feature selection based on the sparsityThreshold setting. Sparsity is here defined as the fraction of samples where a microbial abundance (ASV/OTU or otherwise) is zero. For vanderPloeg2024 we can take the RFgroups groups into account for feature selection. We do this by calculating the sparsity for each feature in each subject group and compare those against the sparsity threshold that we set. If a feature passes the threshold in either group, it is selected.
  • It performs a centered log-ratio transformation of each sample using the compositions::clr() function with a pseudo-count of one (on all features, prior to selection based on sparsity).
  • It centers and scales the three-way array. This is a complex topic that is elaborated upon in our accompanying paper. By centering across the subject mode, we make the subjects comparable to each other within each time point. Scaling within the feature mode avoids the PARAFAC model focusing on features with abnormally high variation.

The outcome of processing is a new version of the dataset. Please refer to the documentation of processDataCube() for more information.

processedPloeg = processDataCube(vanderPloeg2024, sparsityThreshold=0.50, considerGroups=TRUE, groupVariable="RFgroup", CLR=TRUE, centerMode=1, scaleMode=2)

Determining the correct number of components

A critical aspect of PARAFAC modelling is to determine the correct number of components. We have developed the functions assessModelQuality() and assessModelStability() for this purpose. First, we will assess the model quality and specify the minimum and maximum number of components to investigate and the number of randomly initialized models to try for each number of components.

Note: this vignette reflects a minimum working example for analyzing this dataset due to computational limitations in automatic vignette rendering. Hence, we only look at 1-3 components with 5 random initializations each. These settings are not ideal for real datasets. Please refer to the documentation of assessModelQuality() for more information.

# Setup
# For computational purposes we deviate from the default settings
minNumComponents = 1
maxNumComponents = 3
numRepetitions = 5 # number of randomly initialized models
numFolds = 5 # number of jack-knifed models
ctol = 1e-6
maxit = 250
numCores = 1

colourCols = c("RFgroup", "Phylum", "")
legendTitles = c("RF group", "Phylum", "")
xLabels = c("Subject index", "Feature index", "Time index")
legendColNums = c(3,5,0)
arrangeModes = c(TRUE, TRUE, FALSE)
continuousModes = c(FALSE,FALSE,TRUE)

# Assess the metrics to determine the correct number of components
qualityAssessment = assessModelQuality(processedPloeg$data, minNumComponents, maxNumComponents, numRepetitions, ctol=ctol, maxit=maxit, numCores=numCores)

We will now inspect the output plots of interest for vanderPloeg2024.

qualityAssessment$plots$overview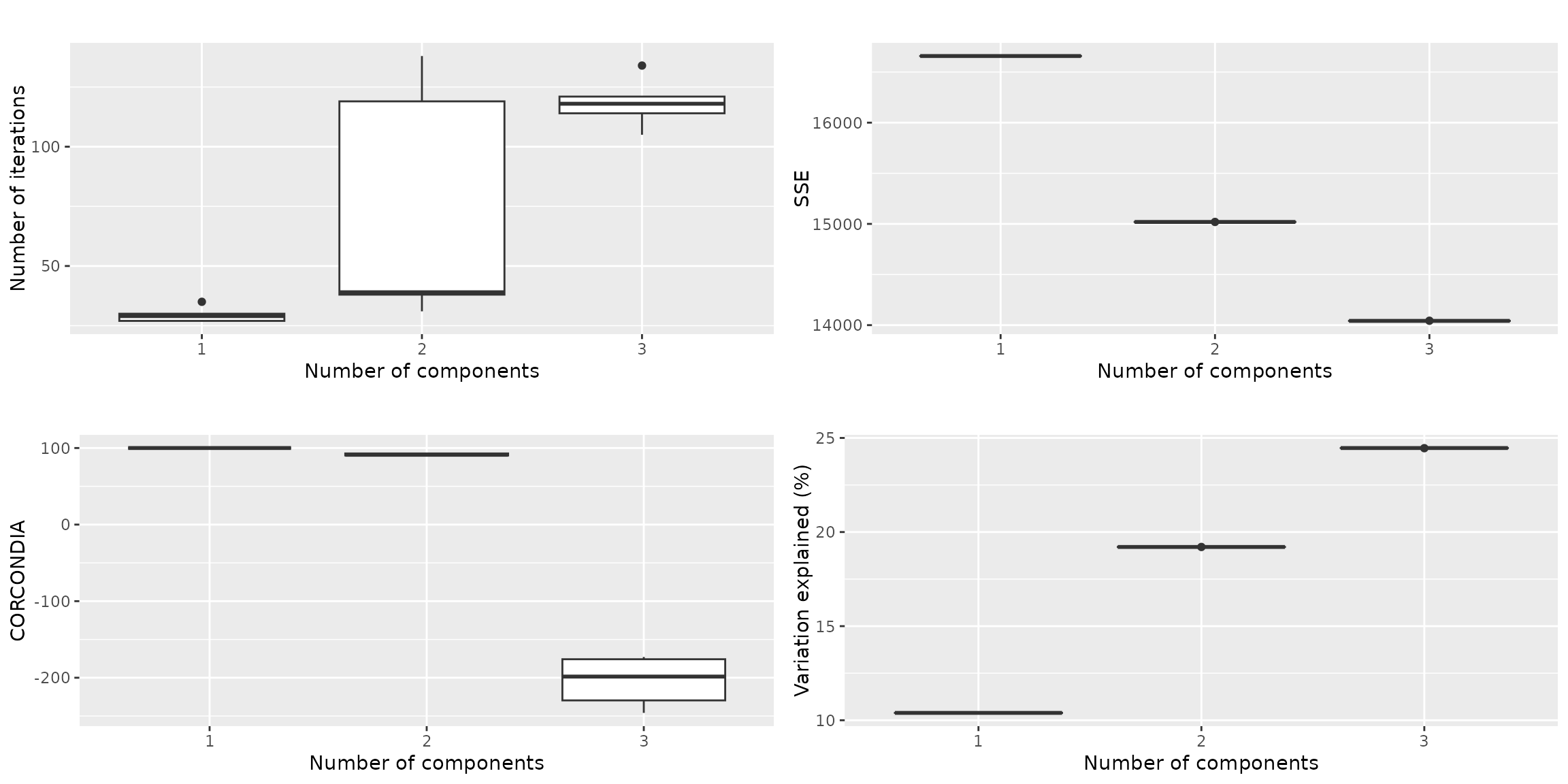

This seems a clear-cut case for a two-component model, as the three-component models have a CORCONDIA of -100. The maximum amount of variation we can describe is ~20%.

Jack-knifed models

Next, we investigate the stability of the models when jack-knifing out samples using assessModelStability(). We briefly inspect the two-component and three-component cases although we already know which will be more appropriate for this data.

stabilityAssessment = assessModelStability(processedPloeg, minNumComponents=1, maxNumComponents=3, numFolds=numFolds, considerGroups=TRUE,
                                           groupVariable="Delivery_mode", colourCols, legendTitles, xLabels, legendColNums, arrangeModes,
                                           ctol=ctol, maxit=maxit, numCores=numCores)

stabilityAssessment$modelPlots[[1]]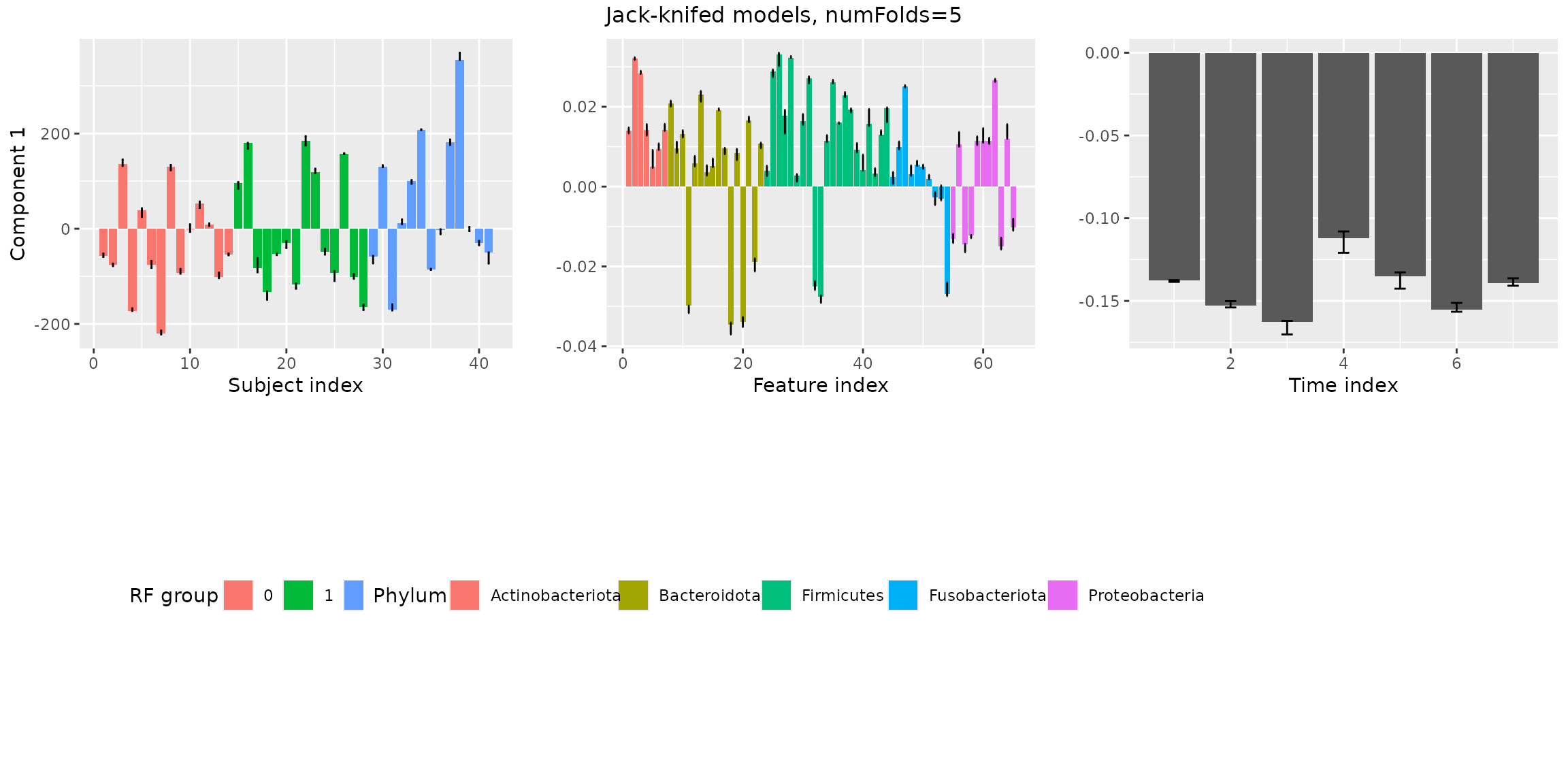

stabilityAssessment$modelPlots[[2]]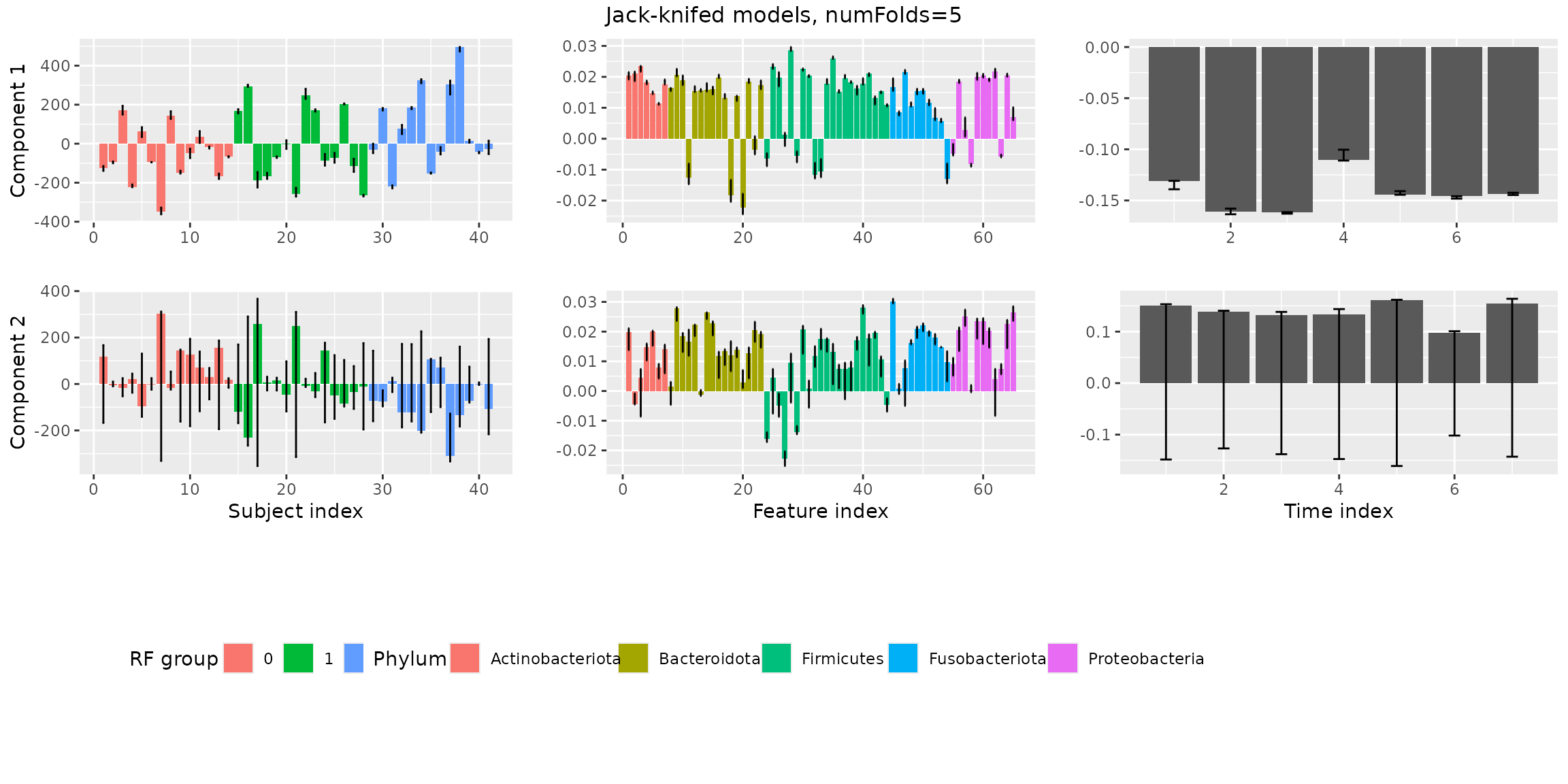

stabilityAssessment$modelPlots[[3]]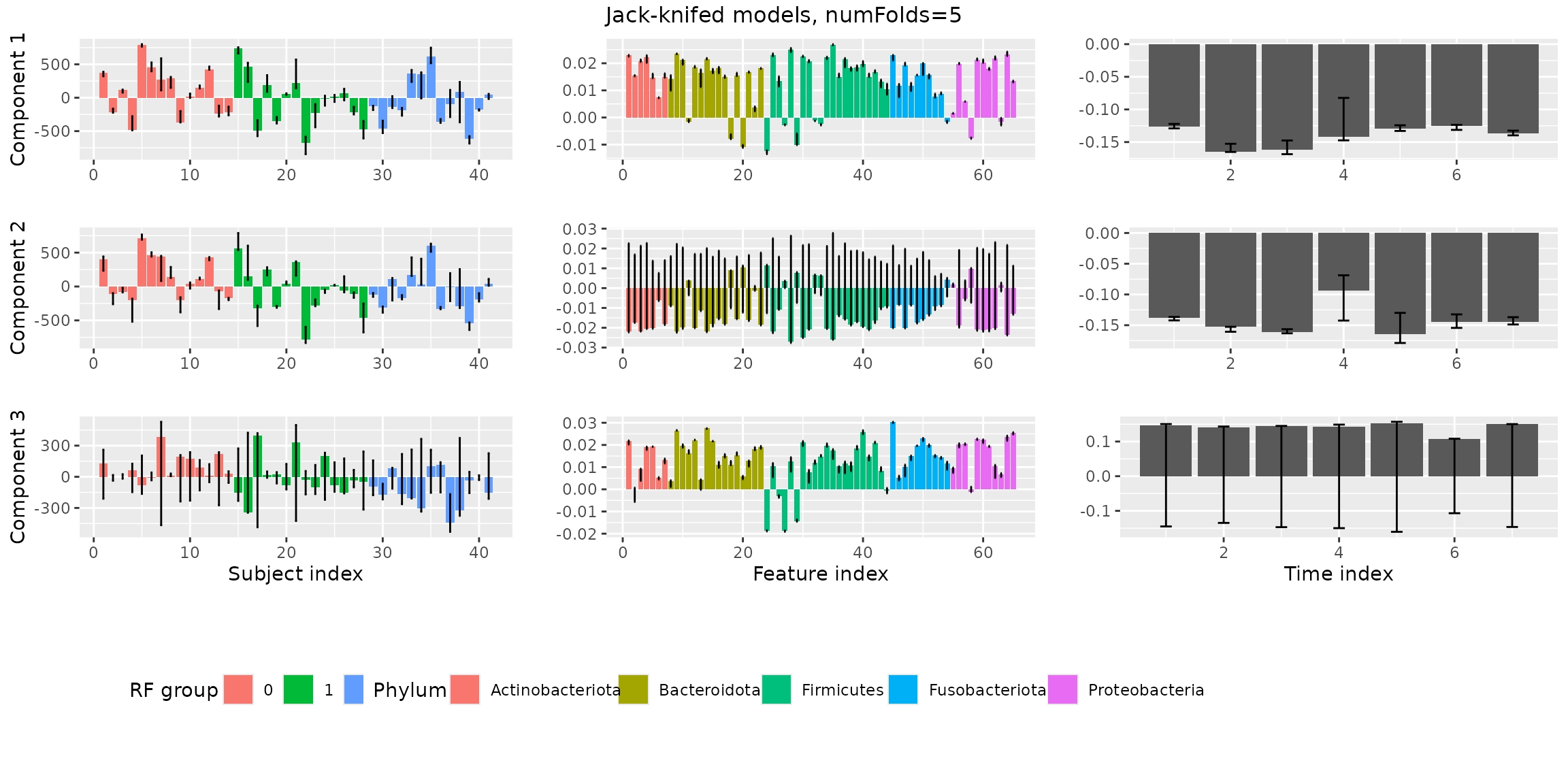

The two-component models are very stable. The three-component models are clearly showing some instability.

Model selection

We have decided that a two-component model is the most appropriate for the vanderPloeg2024 dataset. We can now select one of the random initializations from the assessModelQuality() output as our final model. We’re going to select the random initialization that corresponded the maximum amount of variation explained for two components.

numComponents = 2
modelChoice = which(qualityAssessment$metrics$varExp[,numComponents] == max(qualityAssessment$metrics$varExp[,numComponents]))
finalModel = qualityAssessment$models[[numComponents]][[modelChoice]]

Finally, we visualize the model using plotPARAFACmodel().

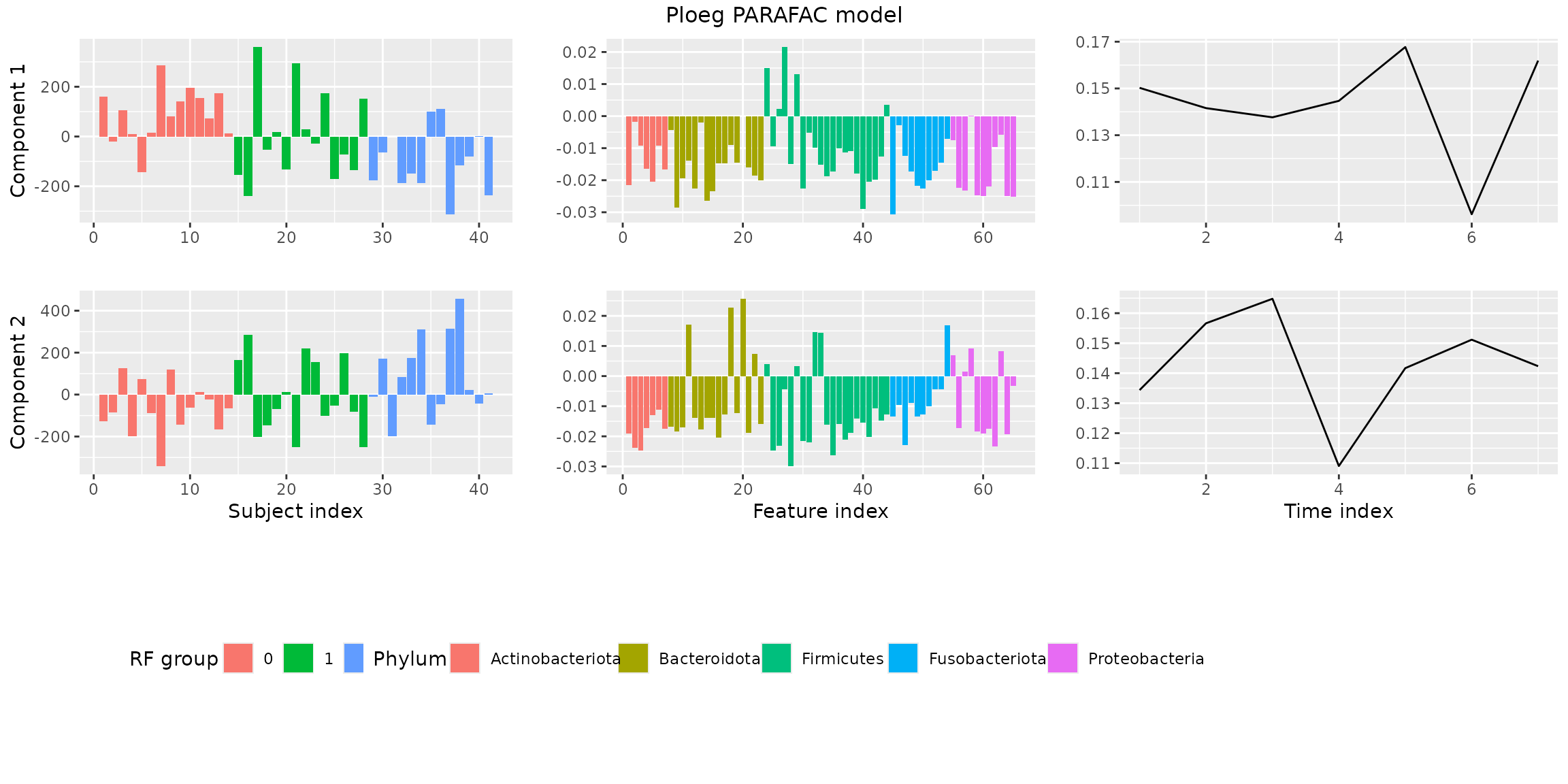
plotPARAFACmodel(finalModel$Fac, processedPloeg, 2, colourCols, legendTitles, xLabels, legendColNums, arrangeModes, continuousModes,
  overallTitle = "vanderPloeg2024 PARAFAC model")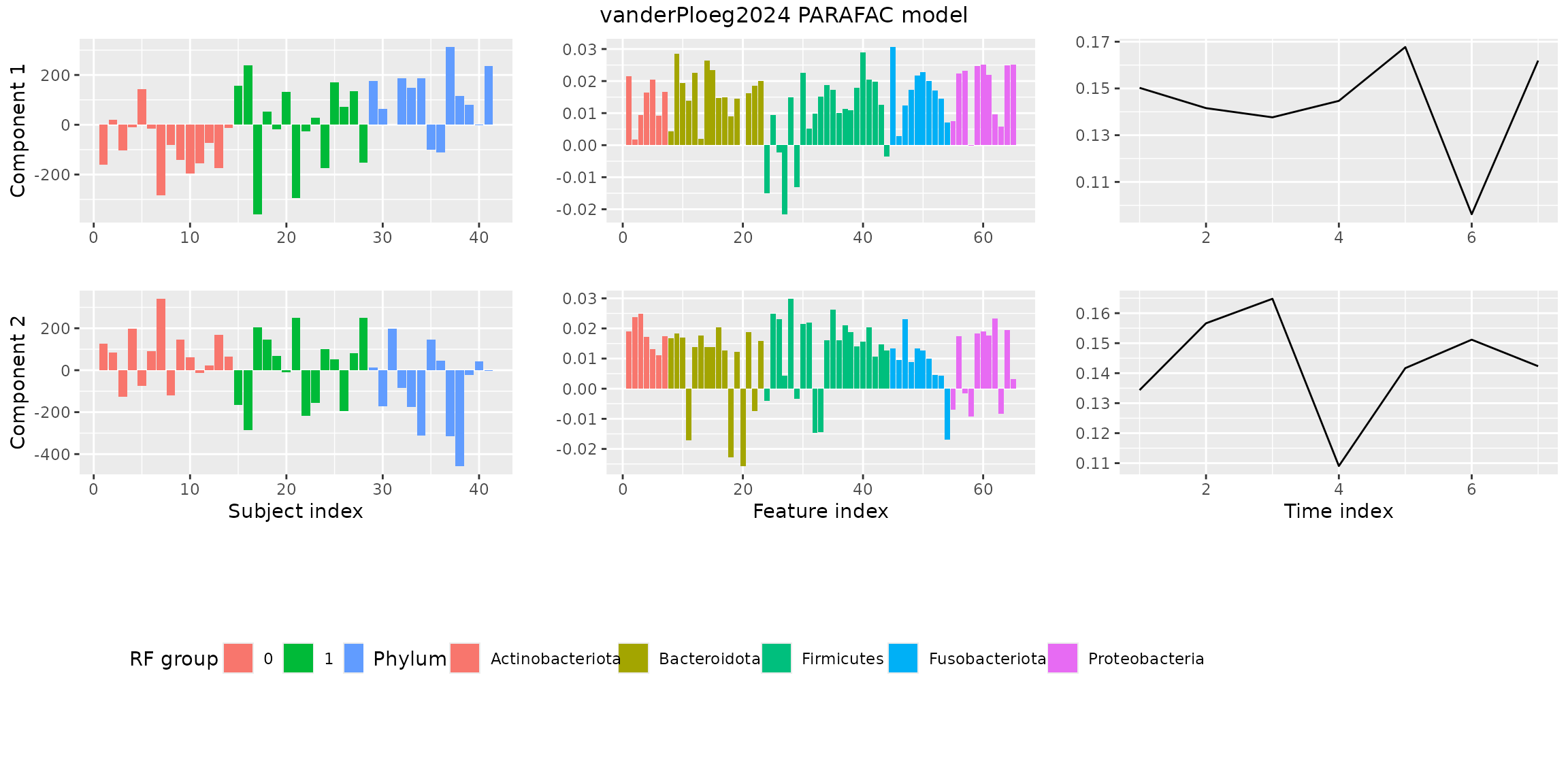

You will observe that the loadings for some modes in some components are negative. This is due to sign flipping: two modes having negative loadings cancel out but describe the same subspace as two positive loadings. We can manually sign flip these loadings to obtain a more interpretable plot.

finalModel$Fac[[1]] = -1 * finalModel$Fac[[1]]         # all of mode 1
finalModel$Fac[[2]] = -1 * finalModel$Fac[[2]]         # all of mode 2

plotPARAFACmodel(finalModel$Fac, processedPloeg, 2, colourCols, legendTitles, xLabels, legendColNums, arrangeModes,
  continuousModes = c(FALSE,FALSE,TRUE),
  overallTitle = "Ploeg PARAFAC model")